Analyse the forces acting on an object executing uniform circular motion in a variety of situations

– cars moving around horizontal circular bends

The only force acting on this car in the horizontal is the force of friction

Hence the frictional force towards the center of the circular path should be equal to , where m is the mass of the car , v is the velocity of the car and r is the radius of the circular path.

-a mass on a string

The circular motion is in a vertical plane.

At every point in the uniform circular motion , the centripetal force acting on the mass must be equal to

The tension in the string at :

point A is T1
point B is T2
point C is T3

At the top point A, the net force is T1+mg. Which implies

At point be B, the downward force is mg, and the inward force towards the center is T2. Hence

At point C, the net force acting is T3 – mg. Hence

-objects on banked tracks

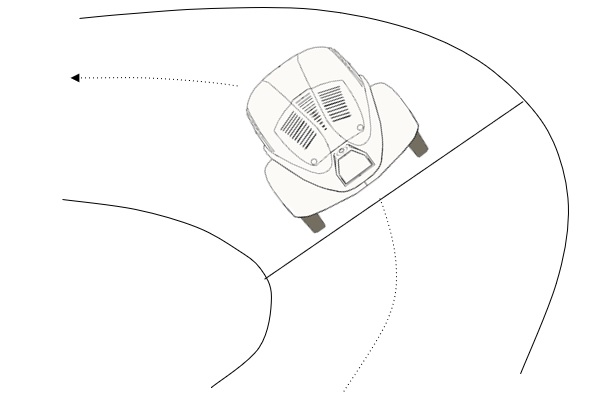
A free body diagram of the car would be as follows:

without friction, the only inward force here is Nx, a component of the Normal force on the car from the road.

Now we know [since there is no motion in the y axis]

centripetal force:

now

which means

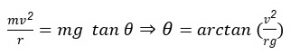
road angle

to achieve speed v, without friction, the roads need to be banked at an angle